\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)

Limits in Maxima

 1 Basic Limits

To take a limit in Maxima, we use the following command:

limit(f(x),x,a)

So, if we wanted to take the limit of f(x)=3x-5 as x approached 6 we would input:

(%i1) limit(3*x-5,x,6);
\[\tag{%o1} 13\]

Or to be very visual about it:

(%i18) limit(3*x-5,x,6);
\[\tag{%o18} 13\]

Of course, we can define a function to do the same:

(%i17) f(x):=x^2 + 5;
L:limit(f(x),x,-2/5);
\[\tag{%o16} \operatorname{f}(x):={{x}^{2}}+5\] \[\tag{L}\frac{129}{25}\]

Here are some other examples:

(%i8) f(x):=(x^2-9)/(x-3);
limit(f(x),x,3);
\[\tag{%o7} \operatorname{f}(x):=\frac{{{x}^{2}}-9}{x-3}\] \[\tag{%o8} 6\]
(%i10) f(x):=(sqrt(x)-2)/(x-4);
limit(f(t),t,4);
\[\tag{%o9} \operatorname{f}(x):=\frac{\sqrt{x}-2}{x-4}\] \[\tag{%o10} \frac{1}{4}\]
-->

Notice in the above example we defined f(x) using x but then swapped the variable for t when we took the limit.
Maxima is not concerned about the name of the variable as long as we are consistent within a command.
Let's push this a little further:

(%i15) f(x):=(x+1)/(x^2-1);
limit(f(y),y,a);
\[\tag{%o14} \operatorname{f}(x):=\frac{x+1}{{{x}^{2}}-1}\] \[\tag{%o15} \frac{1}{a-1}\]

So in addition to being able to do the algebra under a completely different variable (y), Maxima is
smart enough to approach a value that is itself a variable!

 2 Showing What You Typed: The ev(,nouns) Trick

When we define a function in Maxima, wxMaxima is kind enough to show us (in a pretty format) exactly what we typed in.  For example:

(%i19) f(t):=(t^2-2)^3*cos(%e^t);
\[\tag{%o19} \operatorname{f}(t):={{\left( {{t}^{2}}-2\right) }^{3}} \cos{\left( {{\% e}^{t}}\right) }\]

But when we evaluate a limit, it just gives the answer:

(%i20) limit(f(t),t,log(%pi/2));
\[\tag{%o20} 0\]
-->

What if we wanted to make sure that we were typing everything in correctly? Recall that there is a way to make wxMaxima *show* you what you typed in using the (') apostrophe character:

(%i21) 'limit(f(t),t,log(%pi/2));
\[\tag{%o21} \lim_{t\to \log{\left( \frac{\ensuremath{\pi} }{2}\right) }}{{{\left( {{t}^{2}}-2\right) }^{3}} \cos{\left( {{\% e}^{t}}\right) }}\]

That's pretty good, but we can do even better!  We can force wxMaxima to show us our calculation *and* return its value using the ev( ,nouns) trick.

(%i24) f(t):=%e^(1/(t+1))*(t-1)/(t^3-1);
L:'limit(f(t),t,1)$
L=ev(L,nouns);
\[\tag{%o22} \operatorname{f}(t):=\frac{{{\% e}^{\frac{1}{t+1}}}\, \left( t-1\right) }{{{t}^{3}}-1}\] \[\tag{%o24} \lim_{t\to 1}{\frac{\left( t-1\right) \, {{\% e}^{\frac{1}{t+1}}}}{{{t}^{3}}-1}}=\frac{\sqrt{\% e}}{3}\]

Let's see that sequence of events again:

(%i27) h(t):=cos(5*sqrt(t-1))^2$
L:'limit(h(t),t,%pi^2+1)$
L=ev(L,nouns);
\[\tag{%o27} \lim_{t\to {{\ensuremath{\pi} }^{2}}+1}{{{\cos{\left( 5 \sqrt{t-1}\right) }}^{2}}}=1\]

The sequence goes:

1) Define any functions that you are going to be using in your calculation.  You can show it, or you can suppress it with the $

2) Bind to a variable -- in the above L using the (:) the *displayed expression* of the limit you want to compute.

3) Ask Maxima to write out the expression *and* its answer using L = ev(L, nouns)

 2.1 Why the ev(,nouns) Trick Works

Maxima has two primary types of objects: nouns and verbs.  Roughly, nouns are things that are shown to the user and verbs are things that Maxima works on.  Even more roughly, nouns are things that are, while expressions are things that do - just like the distinction between nouns and verbs in English.

When we use the (') apostrophe in a command we type in:

(%i28) N:'limit(5*x^2,x,1);
\[\tag{N}5 \left( \lim_{x\to 1}{{{x}^{2}}}\right) \]

We are telling Maxima that N should be treate as a noun.  But what if we wanted to force the noun to do some work and give us the answer?  This is where ev() comes in:

ev() is Maxima's evaluate command an it works as follows:

ev(EXPRESSION YOU WANT EVALUATED, THING IN THE EXPRESSION YOU WANT DONE)

So if I write:

(%i29) ev(N,nouns);
\[\tag{%o29} 5\]

Maxima interprets this as: find all the nouns in N and make them do work.  By writing:

(%i30) N=ev(N,nouns);
\[\tag{%o30} 5 \left( \lim_{x\to 1}{{{x}^{2}}}\right) =5\]
-->

I get to play both sides:  I see what I typed in and I evaluate it.  From here on out we will use the ev(,nouns) trick to simultaneously display and evaluate our work.

 3 More Limits

 3.1 Expected Behavior

All of the limits we saw previously a) existed, and b) were not infinite.  Let's see how Maxima handles these situations:

(%i32) E:'limit(1/(x-1)^2,x,1)$
E=ev(E,nouns);
\[\tag{%o32} \lim_{x\to 1}{\frac{1}{{{\left( x-1\right) }^{2}}}}=\infty \]

Nice!  How bout  limit that does not exist?

(%i34) E:'limit(sin(1/x),x,0)$
E=ev(E,nouns);
\[\tag{%o34} \lim_{x\to 0}{\sin{\left( \frac{1}{x}\right) }}=\mathit{ind}\]

ind?!!  What the heck is that?!  ind is Maxima's polite way of telling us that the limit is ind-eterminant, or in other words, has no one specific value.  We know that this means that the limit does not exist, but this is a very specific type of not existing.  If we plot the function we can see why this is the case:

(%i35) wxplot2d(sin(1/x),[x,-%pi/12,%pi/12]);
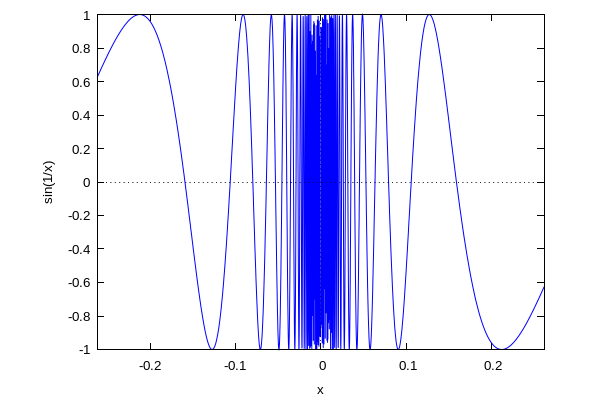
\[\mbox{}\\\mbox{plot2d: expression evaluates to non-numeric value somewhere in plotting range.}\] \[\tag{%t35} \] (Graphics)
\[\tag{%o35} \]

We see that the sin(1/x) function oscillates infinitely fast as we approach 0 from either side so that there is no unique limit of any kind. In short: ind is Maxima's way of saying DNE (Does not exist!)

 3.2 Unexpected Behavior

Let's try another limit that doesn't exist, but this time, let's include a problem with the domain:

(%i37) L:'limit(sqrt(x),x,0)$
L=ev(L,nouns);
\[\tag{%o37} \lim_{x\to 0}{\sqrt{x}}=0\]

What... ?!!  This shouldn't happen.  We, being good Calculus students would expect the limit above to either throw an error, or at least grumble, since the square root can only be approached from the right side of 0! What's going on?!

The issue that we are being confronted with is that Maxima is too smart for its own good. We, as Calculus students are expecting Maxima to evaluate the limit as a Calculus student, not as an expert Mathematician.  But a Mathematician knows that you can take square roots of negative numbers just as well as taking the roots of positive numbers!   And if we approach along the negative real axes we see:

(%i42) sqrt(-1);sqrt(-1/4);sqrt(-1/121);sqrt(-1/625);sqrt(-1/10000);
\[\tag{%o38} \% i\] \[\tag{%o39} \frac{\% i}{2}\] \[\tag{%o40} \frac{\% i}{11}\] \[\tag{%o41} \frac{\% i}{25}\] \[\tag{%o42} \frac{\% i}{100}\]

Notice how all of these are complex numbers, but are also getting smaller?!  Maxima understands this and gives us the more sophisticated view that:

(%i43) limit(sqrt(x),x,0);
\[\tag{%o43} 0\]

Which is true as long as we allow for complex values.  At this point you may cry foul and say: "But I'm a Calculus student and this is *NOT* what the back of the book says!"  Unfortunately, there is no easy way to turn this behavior off.  You must be aware of this when you request two sided limits that require an approach outside of the domain of the square root.

The same must also be said about the logarithm, which also has a well-defined meaning for negative numbers:

The same must also be said about the logarithm, which also has a well-defined meaning for negative numbers:

(%i5) log(-5);realpart(log(-5));imagpart(log(-5));
\[\tag{%o3} \log{\left( -5\right) }\] \[\tag{%o4} \log{(5)}\] \[\tag{%o5} \ensuremath{\pi} \]

You saw that right, what Maxima is telling us is the truth:

(%i7) E:log(-5)$
'E=realpart(E)+imagpart(E)*%i;
\[\tag{%o7} E=\log{(5)}+\% i \ensuremath{\pi} \]

This means that logarithms and square roots both must be handled *very* carefully!

 4 Limits at Infinity

Maxima understands inf as "infinity" and minf as "negative infinity".  In this way:

(%i9) H:'limit(1/sqrt(x),x,inf)$
H=ev(H,nouns);
\[\tag{%o9} \lim_{x\to \infty }{\frac{1}{\sqrt{x}}}=0\]
(%i11) H:'limit((3*x^2+2*x+1)/(5-6*x+7*x^2),x,minf)$
H=ev(H,nouns);
\[\tag{%o11} \lim_{x\to -\infty }{\frac{3 {{x}^{2}}+2 x+1}{7 {{x}^{2}}-6 x+5}}=\frac{3}{7}\]
(%i13) H:'limit(sqrt(exp(-x)+5),x,minf)$
H=ev(H,nouns);
\[\tag{%o13} \lim_{x\to -\infty }{\sqrt{{{\% e}^{-x}}+5}}=\infty \]
-->

 4.1 Want to See Both Limits at Infinit at Once?

Sometimes we would like to see both limits at either end of the real line.  To accomplish this efficiently,
we exploit the fact that we can define a function using the target infinity as the input:

(%i16) H(a):='limit(sqrt(exp(-x)+5),x,a)$
H(inf)=ev(H(inf),nouns);
H(minf)=ev(H(minf),nouns);
\[\tag{%o15} \lim_{x\to \infty }{\sqrt{{{\% e}^{-x}}+5}}=\sqrt{5}\] \[\tag{%o16} \lim_{x\to -\infty }{\sqrt{{{\% e}^{-x}}+5}}=\infty \]

 5 Sided Limits

To tell Maxima to use a left-sided limit, we include the word "minus" at the end of the limit command like so:

(%i18) L:'limit(1/(x-1),x,1,minus)$
L=ev(L,nouns);
\[\tag{%o18} \lim_{x\to 1-}{\frac{1}{x-1}}=-\infty \]

To get a right-sided limit we add in the word "plus":

(%i20) L:'limit(1/(x-1),x,1,plus)$
L=ev(L,nouns);
\[\tag{%o20} \lim_{x\to 1+}{\frac{1}{x-1}}=\infty \]
Created with wxMaxima.